The most
used topic of mathematics in our life without knowing is function. So in this
article we will talk about function, what is function, its types and many
simple examples of function we use in our daily life.
Function And its Type
Function in
simple meaning is something that gives output when you give something input. It
is exactly similar to the mill when you give certain grain to input you will
get flour as output. We can compare uniqueness of mill to function, that is if
you put wheat to input you will get wheat flour as output you never get maze
flour as output similarly in function you will get always unique output to
given input.
In
mathematical terms;
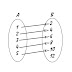
A relation that uniquely associates members of one set with members of
another set is known as function. More formally, a function from a set X to Y is an operation f such
that for every x belonging to the set X is uniquely associated with f(x)
belonging to Y. Where f(x) is also an element of Y.
 |
FIG: Function
|
Notation:
Normally we
use f for the notation of function, or we can use letter like g or certain
names also like squaring.
Examples:
- X2 (square) is a function
- Sine, Cosine and Tangent are some function of trigonometry.
Types of function:
Generally,
there are various types of function we will discuss main type of function here:
1. Injective function or One to one
function:
A function that
preserves its distinctness is known as Injective or One to one function; it never maps distinct elements of one set namely domain
to the same elements of another set namely co-domain.
Here the
function is injective in since every unique element of X that is domain has
unique element in Co-domain.
But here
for element 3 and 4 of X has same image in Y so is not injective function. That
is there must be unique image for unique element.
2. Surjective function or Onto function
In mathematics a function from a set X to set Y is said to be Surjective
or Onto function if for every element in y in Y of f there is at least one
element x in X of f such that; f(x)=y. Here it is not necessary that x is
unique.
Here
for every element of Y there is at least one element in X so is surjective
function.
3. Bijective function:
A
function is said to be bijective function, if it is both surjective and
injective. Some time it is also known as One to one correspondence.
4. Identity function:
A function is said to be Identity function if it maps any given elements
to itself. Mathematically,
f(x)=x is Identity function.
5. Constant function:
A function or map is said to be constant function if it maps every
element of domain to same element on the codomain.
Mathematically,
f(x)=4 is constant function.
Hope you get some idea what the function is so see you in the next article.











0 comments: